ФЕРМА (Fermat) Пьер (1601-65) - французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).
ферма (в строительстве)
Энциклопедический словарь
ФЕРМА (в строительстве) - ФЕ́РМА (франц. ferme, от лат. firmus - прочный), в строительной механике - геометрически неизменяемая стержневая система, у которой все узлы принимаются при расчете шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, мостах и др.
Полезные сервисы
ферма (с/х предприятие)
Иллюстрированный энциклопедический словарь
ФЕРМА, индивидуальное сельскохозяйственное предприятие, ведущееся на собственной или арендованной земле с целью получения товарной сельскохозяйственной продукции и денежного дохода; связано, как правило, с поселением хуторского типа. В современных условиях в развитых странах многие фермерские хозяйства втягиваются в систему межотраслевых связей, организуемых промышленными предприятиями и кооперативами на основе вертикальной интеграции, становясь при этом частями крупных агропромышленных объединений.
Полезные сервисы
ферма (строит.)
Иллюстрированный энциклопедический словарь
ФЕРМА (от латинского firmus - прочный) (строительное), стержневая несущая конструкция, у которой соединения стержней в узлах при расчете принимаются шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, пролетных строениях мостов, гидротехнических сооружениях и др.
Полезные сервисы
ферма принцип
Энциклопедический словарь
ФЕРМА ПРИНЦИП - ФЕРМА́ ПРИ́НЦИП: действительный путь распространения света из одной точки в другую есть тот путь, для прохождения которого свету требуется минимальное (или максимальное) время по сравнению с любым др. геометрически возможным путем между теми же точками. Установлен П. Ферма ок. 1660.
Большой энциклопедический словарь
ФЕРМА ПРИНЦИП: действительный путь распространения света из одной точки в другую есть тот путь - для прохождения которого свету требуется минимальное (или максимальное) время по сравнению с любым др. геометрически возможным путем между теми же точками. Установлен П. Ферма ок. 1660.
Полезные сервисы
ферма принцип{:}
Энциклопедический словарь
Ферма́ при́нцип{:} - действительный путь распространения света из одной точки в другую есть тот путь, для прохождения которого свету требуется минимальное (или максимальное) время по сравнению с любым другим геометрически возможным путём между теми же точками. Установлен принцип Ферма около 1660.
Полезные сервисы
ферма пьер
Энциклопедический словарь
Ферма́ Пьер (Fermat) (1601-1665), французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).
* * *
ФЕРМА Пьер - ФЕРМА́ (Fermat) Пьер (1601-65), французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).
Энциклопедия Кольера
ФЕРМА Пьер (Fermat, Pierre)
(1601-1665), французский математик, создатель теории чисел и один из основателей математического анализа. Родился 20 августа 1601 в Бомон-де-Ломане. Будучи по профессии юристом, состоял на государственной службе: с 1631 по 1648 был уполномоченным по приему прошений, а с 1648 и до конца жизни - советником парламента Тулузы. Был известен как знаток классической литературы, лингвист и поэт. Математика всегда была для Ферма лишь увлечением, и тем не менее он заложил основы многих ее областей: аналитической геометрии, исчисления бесконечно малых, теории вероятностей. Ферма не оставил ни одной законченной работы, и большинство его набросков не было опубликовано при жизни. Ферма переписывался с Р.Декартом по вопросам аналитической геометрии и был первым, кто воспользовался ее методами применительно к трехмерному пространству. С именем Ферма связаны две знаменитые теоремы из области теории чисел: малая теорема Ферма и "великая" теорема Ферма, о которой на полях трудов Диофанта он написал: "Я нашел этому поистине чудесное доказательство, но эти поля слишком малы для него". Согласно этой теореме, уравнение
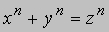
, где n > 2 не имеет целых положительных корней. Ее доказательство в общем виде было получено лишь в 1994. Идеи и открытия Ферма в области теории чисел оказали колоссальное влияние на последующие поколения математиков. Умер Ферма в Кастре близ Тулузы 12 января 1665.
ЛИТЕРАТУРА
Хинчин А.Я. Великая теорема Ферма. М. - Л., 1932 Эдвардс Г. Последняя теорема Ферма. М., 1980
Полезные сервисы
ферма стропильная
ферма теорема
Энциклопедический словарь
Ферма́ теоре́ма - утверждение теории чисел, согласно которому уравнение xn + yn = zn при n > 2 не имеет целых положительных решений. Справедливость Ферма теоремы доказана для ряда показателей n, но в общем виде остаётся недоказанной. П. Ферма, высказавший эту теорему, не оставил её доказательства.
* * *
ФЕРМА ТЕОРЕМА - ФЕРМА́ ТЕОРЕ́МА, утверждение теории чисел, согласно которому уравнение xn+yn=zn при n>2 не имеет целых положительных решений. Справедливость теоремы Ферма доказана для ряда показателей n, но в общем виде остается недоказанной. П. Ферма, высказавший эту теорему, не оставил ее доказательства. Долгое время справедливость теоремы Ферма было доказано только для ряда показателей n. В общем виде доказательство теоремы было представлено в 1995 году английским математиком Э. Уайлзом.
Большой энциклопедический словарь
ФЕРМА ТЕОРЕМА - утверждение теории чисел, согласно которому уравнение xn+yn=zn при n"2 не имеет целых положительных решений. Справедливость теоремы Ферма доказана для ряда показателей n, но в общем виде остается недоказанной. П. Ферма, высказавший эту теорему, не оставил ее доказательства.
Иллюстрированный энциклопедический словарь
ФЕРМА ТЕОРЕМА, утверждение теории чисел, согласно которому уравнение xn+yn=zn при n > 2 не имеет целых положительных решений. П. Ферма, высказавший эту теорему, не оставил ее доказательства. Эндрю Уайлз (Andrew Wiles), математик из Принстона, привел в 1994 г. полное доказательство теоремы Ферма. Проверка доказательства, основанного на теореме Фальтингса, завершена к 1996 году.